Thesis: Structuring the hydrodynamics of the Elbe estuary
- Partners
- University of Twente
- Researcher
- Karla Korporaal
Estuaries serve crucial functions, such as acting as shipping routes that connect the sea to ports. Understanding the complex hydrodynamics of estuaries is essential for managing these vital systems, especially when planning interventions, assessing risks, or dealing with critical situations. Numerical models are important tools for simulating future scenarios. These hydrodynamic simulations provide insights into processes such as tidal movements, changes in water levels, and assessing the impact of interventions. This thesis research by Karla Korporaal contributes to improving the use of numerical models in the complex field of estuarine hydrodynamics, with a focus on the sensitivity of grid choices in subgrid-based numerical hydrodynamic models to accuracy. The research supports the development of strategies for grid choices when modeling estuaries.
The challenge
Subgrid techniques allow for the use of a lower resolution computational grid with minimal loss of accuracy. Additionally, subgrid methods enable the use of structured grids due to automatic inundation within a computational cell, eliminating the need for the grid to follow land-sea boundaries. However, in dynamic areas of an estuary, it may be important to choose a higher resolution for the computational grid. This higher resolution can better simulate dynamic flows but leads to longer computation times. Striking a balance between minimizing computation times and ensuring accuracy is a delicate trade-off that must always be considered. By using a structured, non-uniform grid, such as a quadtree, it is possible to locally increase the grid resolution with only a slight increase in computation time. This raises the question of where these local refinements to the computational grid should be applied.
Our solution
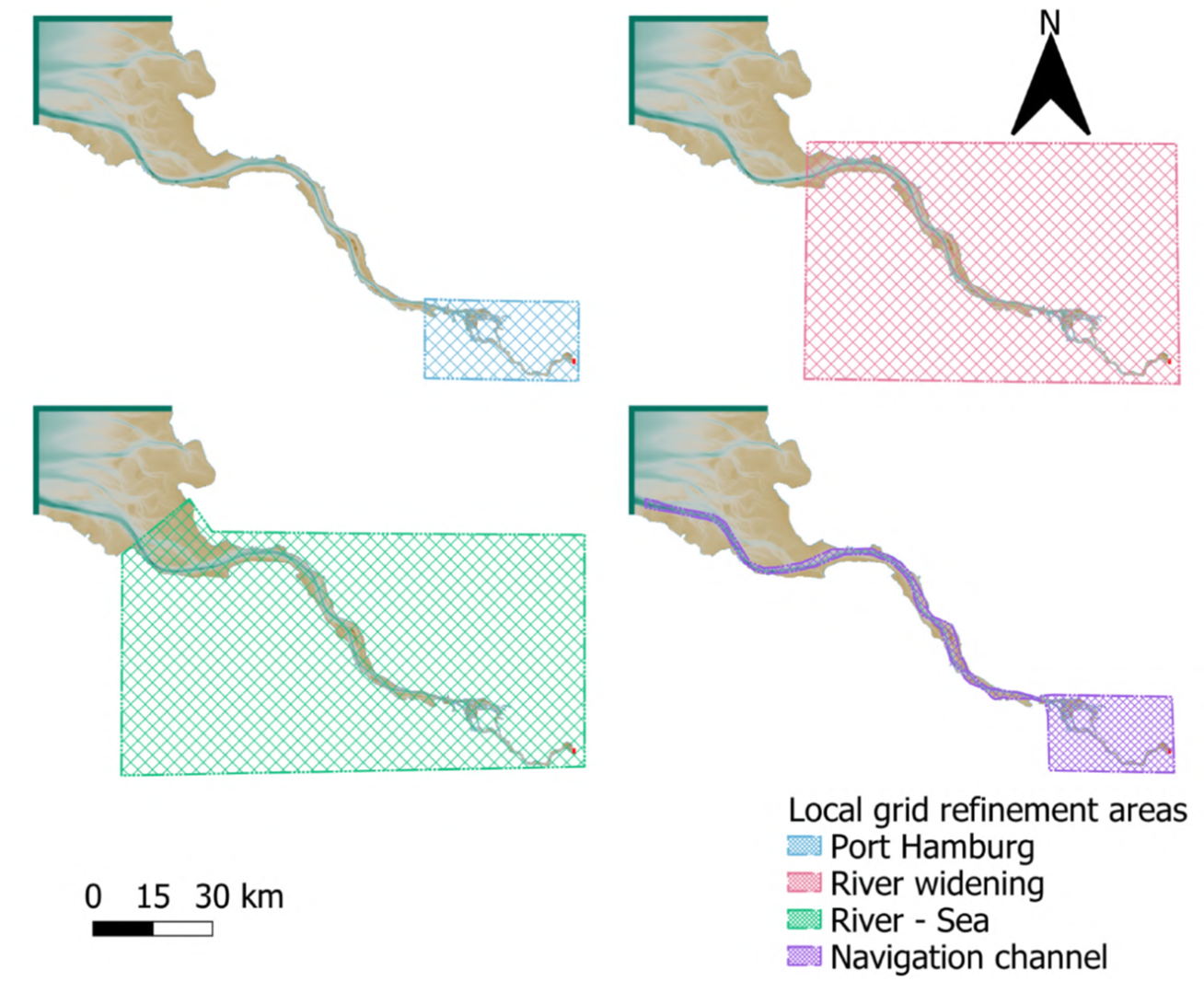
The research aimed to map the sensitivity of key modeling choices when applying subgrid methods in combination with structured, non-uniform grids. It highlighted the critical importance of a strong alignment between tidal boundary conditions and grid configuration. Additionally, it examined how the use of non-uniform grids with local refinements can improve both model accuracy and computational efficiency. Strategically placed refinements in complex flow areas, such as river widening zones and the main navigation channel, can enhance hydrodynamic results. A lower-resolution grid can be used in open sea areas, provided that critical zones are sufficiently refined. While refinements improve accuracy in specific areas, they can also increase computation times as the number of grid points grows. Striking a balance between grid resolution and local refinements remains essential. For the Elbe estuary, refining the navigation channel is of particular importance.
The outcome
The potential of using subgrid techniques combined with structured, non-uniform grids for large-scale estuarine studies was confirmed, as it accurately captured the hydrodynamics of the Elbe estuary with deviations of less than 10 cm compared to measurements. Moreover, through strategically placed refinements, a 15-day simulation can be completed in just 5 minutes of computation time.